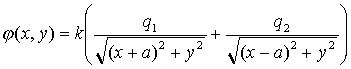|

|

|

|
| |
| Сивухин | §17-22; |
| Савельев | §6,11,12; |
| Гершензон | §1.6,1.7;1.9 |
| Трофимова | §83-86; |
| БКФ | §2.2-2.5;2.12 |
| Калашников | §16, 24 |




ЛЕКЦИЯ №7
ПОТЕНЦИАЛ ЭЛЕКТРИЧЕСКОГО ПОЛЯ (продолжение)
|
Чтобы узнать вещь, нужно ее сделать. Ибо хотя вы думаете, что знаете ее, в этом не может быть уверенности, пока вы не попытаетесь ее сделать. (Софокл) |
В предыдущей лекции мы ввели для характеристики электростатического
поля скалярный потенциал j. При этом было сказано,
что потенциал является энергетической характеристикой электростатического поля,
и описание с помощью него свойств поля полностью эквивалентно описанию с помощью
напряжённости, являющейся силовой характеристикой этого поля. Рассмотрим теперь
более подробно, как связаны друг с другом данные величины. Поскольку в каждой
точке пространства у нас теперь помимо вектора  задано
значение скалярной функции
задано
значение скалярной функции  , то есть
кроме векторного поля оказывается, определено ещё скалярное, то рассмотрим вначале
некоторые сведения из математической теории поля, касающиеся скалярных полей
– их структуры и характеристик.
, то есть
кроме векторного поля оказывается, определено ещё скалярное, то рассмотрим вначале
некоторые сведения из математической теории поля, касающиеся скалярных полей
– их структуры и характеристик.
1. Скалярные поля. Понятие градиента(математическое отступление).
 |
def: Если в каждой точке области пространства V задано некоторое число
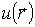 , то говорят,
что в этой области пространства определено скалярное поле. , то говорят,
что в этой области пространства определено скалярное поле.
|
 |
def: Геометрическое место точек, для которых величина u принимает одно и тоже числовое значение С, называется поверхностью уровня, соответствующей числу С. Уравнение этой поверхности: u(x,y,z)=С. |
Очевидно, что поверхности уровня, отвечающие различным С заполняют всю область пространства, в которой определено скалярное поле. При этом никакие две поверхности не пересекаются.
Отметим, что плоское поле u(x,y) может быть задано линиями уровня, соответствующими уравнениям вида u(x,y)=C.
Таким образом, структура скалярного поля гораздо проще структуры векторных полей, в которых имеются такие образования как источники поля и различные завихрённости. Скалярное же поле всё состоит из поверхностей уровня и, если мы находимся в некоторой точке пространства, то помимо того к какой поверхности уровня принадлежит эта точка (чему равно значение функции u в этой точке) нас может интересовать ещё только вопрос о том как будет вести себя функция u при смещении из данной точки в соседние – будет ли она возрастать или убывать и сколь быстро. Для ответа на этот вопрос вводят понятие производной по направлению.
Эта «пространственная» производная определяется аналогично обыкновенной.
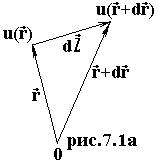 А именно:
если мы из точки радиус–вектор которой
А именно:
если мы из точки радиус–вектор которой 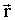 сместимся в произвольном направлении на бесконечно малый вектор
сместимся в произвольном направлении на бесконечно малый вектор 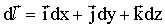 (рис.7.1а), то значения функции u при этом также изменятся на
бесконечно малую величину
(рис.7.1а), то значения функции u при этом также изменятся на
бесконечно малую величину 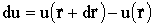 ,
определяемую, в соответствии с формулой полного дифференциала функции трёх переменных
выражением:
,
определяемую, в соответствии с формулой полного дифференциала функции трёх переменных
выражением: 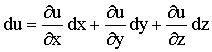 .
Учитывая формулу для
.
Учитывая формулу для 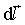 ,
данное выражение можно рассматривать как скалярное произведение двух векторов:
,
данное выражение можно рассматривать как скалярное произведение двух векторов:
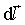 и вектора с
компонентами
и вектора с
компонентами
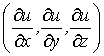 .
.
Этот вектор называется градиентом скалярного поля u, и обозначается: gradu.
Таким образом,  . Производная
же поля u по направлению,
определяемому вектором
. Производная
же поля u по направлению,
определяемому вектором 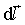 , может
быть формально получена как отношение изменения функции du
к расстоянию, на котором это изменение произошло, то есть к
, может
быть формально получена как отношение изменения функции du
к расстоянию, на котором это изменение произошло, то есть к 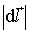 (разумеется,
более строго как соответствующий предельный переход):
(разумеется,
более строго как соответствующий предельный переход):
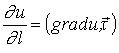 , где
, где 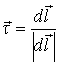 , (7.1)
, (7.1)
- единичный вектор, определяющий направление, в котором вычисляется производная (7.1). Так как в соответствии с определением скалярного произведения
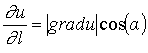 ,
,
где a - угол между gradu и
вектором 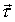 . Значит, градиент, это
вектор, в направлении которого функция u будет расти с наибольшей
скоростью. Производная же функции u в произвольном направлении,
определяемом единичным вектором
. Значит, градиент, это
вектор, в направлении которого функция u будет расти с наибольшей
скоростью. Производная же функции u в произвольном направлении,
определяемом единичным вектором 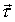 равна, в соответствии с (7.1) проекции gradu на это направление.
равна, в соответствии с (7.1) проекции gradu на это направление.
 Рассмотрим теперь,
как связаны друг с другом поверхности уровня и градиенты скалярных полей. Для
этого заметим, что если мы сместимся из данной точки пространства на вектор
Рассмотрим теперь,
как связаны друг с другом поверхности уровня и градиенты скалярных полей. Для
этого заметим, что если мы сместимся из данной точки пространства на вектор
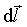 вдоль поверхности уровня, на которой
эта точка лежит (рис.7.1б), то функция u при этом не изменится,
то есть du=0. Следовательно,
вдоль поверхности уровня, на которой
эта точка лежит (рис.7.1б), то функция u при этом не изменится,
то есть du=0. Следовательно, 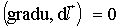 , что возможно,
если только
, что возможно,
если только 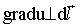 . Отсюда
следует, что градиент скалярного поля перпендикулярен к поверхности уровня в
каждой её точке, а это в свою очередь означает, что скалярное поле наиболее
быстро растёт в направлении нормали
. Отсюда
следует, что градиент скалярного поля перпендикулярен к поверхности уровня в
каждой её точке, а это в свою очередь означает, что скалярное поле наиболее
быстро растёт в направлении нормали 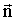 к поверхности
уровня, и соответственно, убывает в направлении
к поверхности
уровня, и соответственно, убывает в направлении 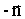 .
.
Резюмируя всё сказанное, дадим следующее определение.
 |
def: Градиентом скалярной функции u(x,y,z) называется
вектор, направленный в сторону максимального возрастания этой функции в
данной точке пространства, а его длина равна производной функции в том же
направлении.
(Название - от латинского слова gradiens – шагающий). |
Таким образом, для характеристики локальных свойств скалярных полей вводится всего один дифференциальный оператор – градиент, который и содержит в себе всю необходимую информацию об этих полях. Для характеристики же локальных свойств векторных полей (для описания источников и завихрений в этих полях) вводится два дифференциальных оператора – дивергенция и ротор, что ещё раз подчёркивает сложность их структуры в сравнении со скалярными полями.
Следует отметить, что термины и обозначения «дивергенция, градиент, ротор» ввел Максвелл (1873). Именно ему мы обязаны изучением столь сложных вещей.
 |
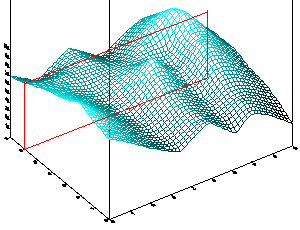
Рассмотренное выше понятие градиента скалярной функции может быть хорошо проиллюстрировано на следующем примере. Предположим, что мы имеем дело с функцией только двух переменных u=u(x,y), то есть у нас есть, фактически плоское скалярное поле. Поэтому значения данной функции могу быть представлены некоторой поверхностью в трехмерной системе координат (рис.7.2а). |
Стоя на этой поверхности, мы видим, что она в одних направлениях поднимается, а в других опускается. В одном из направлений за один короткий шаг мы поднимаемся выше, чем за шаг той же длины в любом другом направлении. (При этом длина шага измеряется, разумеется, в плоскости XOY)
 |
Градиент функции u в нашем случае, это вектор, совпадающий по направлению с наибольшей крутизной, а его модуль равен наклону, измеренному в этом направлении (то есть тангенсу угла, между этим вектором и его проекцией на плоскость X0Y). Характер распределения градиента показан на рис.7.2б небольшим количеством векторов в разных точках данной плоскости |
2. Градиент в различных системах координат(математическое отступление).
В декартовой 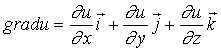
В цилиндрической 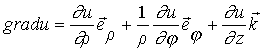
В сферической 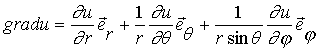
3. Связь напряженности и потенциала электростатического поля.
Напомним, что 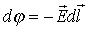 .
С другой стороны (по аналогии с предыдущим пунктом)
.
С другой стороны (по аналогии с предыдущим пунктом) 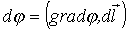 .
Сравнивая выражения, находим, что
.
Сравнивая выражения, находим, что
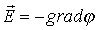 (7.8)
(7.8)
Вектор напряженности показывает направление наиболее быстрого убывания потенциала.
 |
Предположим, что нам дан план какой-либо местности: в озеро впадает река и рядом гора (рис.7.3). Соединим на этом плане точки одинаковой высоты линиями, причем высоты будем брать через одинаковый интервал, например, 1 м. По такому плану легко определить уклон местности между двумя соседними точками: поделить разность уровней между точками на расстояние между ними. Очевидно, что уклон будет больше там, где линии одного уровня ближе друг к другу. |
 |
Это ясно видно и из вертикального разреза местности, сделанного по выделенной на рис.7.3 прямой, что показано на рис.7.4. В какой-нибудь данной точке мы получим наибольший уклон, проведя линию перпендикулярную горизонтали. По таким уклонам и будет стекать вода в данной местности во время дождя. |
Вернемся к электричеству. Поверхности уровня в электростатике, или, соответственно, поверхности одинакового потенциала называется эквипотенциальными (от лат. aequus - равный). Их сечения какой-либо плоскостью будем называть эквипотенциальными линями. Тогда в нашем примере горизонтальные линии – это эквипотенциальные линии, уклоны – разности потенциалов, а линии течения воды – линии напряженности. Именно по ним и будут двигаться электрические заряды.
Ясно, что вектор напряженности и эквипотенциальная поверхность перпендикулярны. Обычно эквипотенциальные поверхности (точнее линии) чертят через одинаковую разность потенциалов.
Заметим, что нулевой потенциал выбираем весьма условно. Смысл имеет разность потенциалов. Также как на местности предметом непосредственного наблюдения является разность уровней, и любой из них можно принять за основной.
 |
rem: Для проводников эквипотенциальная поверхность вырождается в эквипотенциальный объем. |
4. Эквипотенциальные линии двух точечных зарядов.
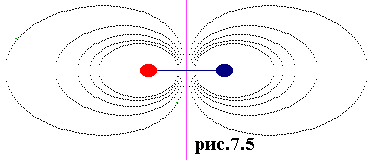 |
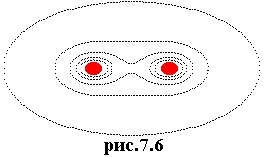
На рис.7.5 показаны рассчитанные эквипотенциальные линии двух одинаковых по модулю, но разных по знаку зарядов. На рис.7.6 то же для одноименных зарядов. |
 |
|
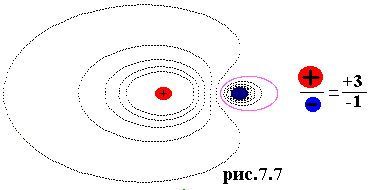
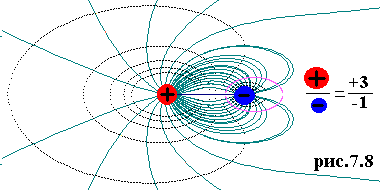
На рис.7.7 показаны эквипотенциальные линии для разноименных неодинаковых по модулю зарядов. Данные построения полезно сравнить с картинами силовых линий (см. рис.4.6-4.7), чтобы убедиться в их ортогональности. Наконец на рисунке 7.8 линии напряженности электростатического поля и эквипотенциальные линии показаны одновременно. |
 |
 |
Рассмотрим теперь ряд расчетных примеров для сравнительно простых геометрий.
5. Потенциал бесконечной заряженной плоскости.
Напряженность ранее была вычислена (5.11). Зная (7.8), имеем
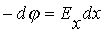
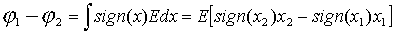
полагая потенциал на плоскости равным нулю, получаем (рис.7.9)
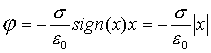 (7.11) (7.11) |
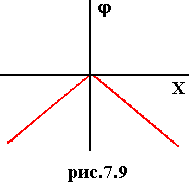 |
6. Потенциал двух бесконечных разноименно заряженных плоскостей.
Выражение для напряженности знаем (5.12). Поступая аналогично предыдущему пункту
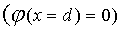 ,
,сразу получаем (рис.7.10)
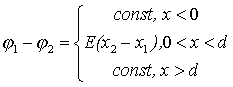
|
или |
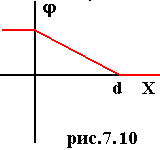 |
Оба случая достаточно экзотические. Попробуйте рассчитать все то же самое при конечных размерах, например, круглых равномерно заряженных пластин. Это не так трудно, как кажется.
7. Потенциал равномерно заряженной сферы.
Задача сферически симметрична, поэтому ясно, что 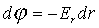 .
Выражение для напряженности знаем (5.13). Вне сферы
.
Выражение для напряженности знаем (5.13). Вне сферы
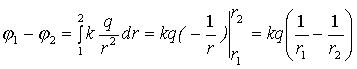
Внутри сферы поля нет, поэтому потенциал постоянен. Сшивая значения потенциала на границе (на бесконечности- 0), получаем (7.17), график на рис.7.11.
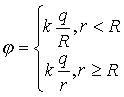 (7.17) (7.17) |
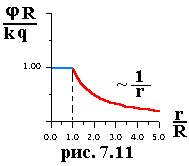 |
8. Потенциал равномерно заряженного шара.
Напряженность знаем (5.14). Вне шара все аналогично сфере. Внутри
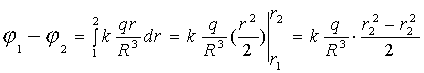
Сшивая значения потенциала на границе, получаем (7.19) (на бесконечности-0). График на рис.7.12
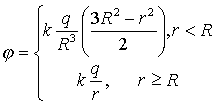 (7.19) (7.19) |
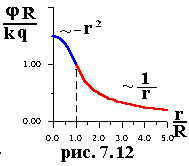 |
9. Потенциал равномерно заряженного бесконечно длинного цилиндра.
Задача имеет цилиндрическую симметрию. Напряженность знаем (5.9). Внутри цилиндра расчет аналогичен шару
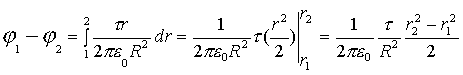
Вне цилиндра
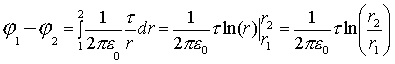
В итоге получаем (считая, что 
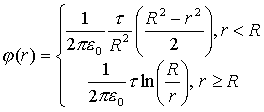 (7.22) (7.22) |
 |
Особенно ясно видно, что смысл имеет разность потенциалов, а не сам потенциал (под оператором функции логарифма должна стоять безразмерная величина). График на рис.7.13. Согласитесь, что это очень похоже на профиль земной поверхности с рис.7.4.
 |
rem: В случаях бесконечных распределений зарядов глупо относить нулевой потенциал на бесконечность, так как и там есть заряды. Поэтому в таких случаях лучше располагать нуль где-нибудь поближе. |
10. Потенциал равномерно заряженной тонкой нити конечной длины.
Общая длина нити l=l1+l2, линейная плотность заряда t (см.рис.7.14)
Используем формулу для расчета потенциала заряженного тела (6.23)
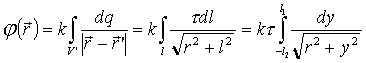
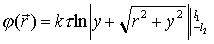
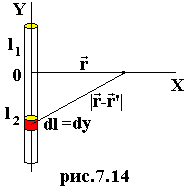 |
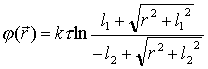 (7.24) (7.24) |
если l1,l2>>r, т.е. нить бесконечна,
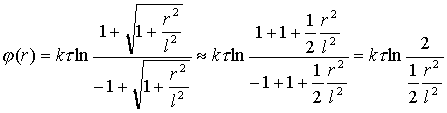
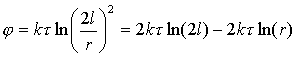
Xорошо видно, что смысл имеет не сам потенциал, а разность потенциалов
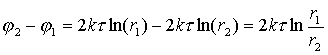 (7.27)
(7.27)что совпадает с формулой (7.22) для наружной области цилиндра.
11. Поверхность нулевого потенциала.
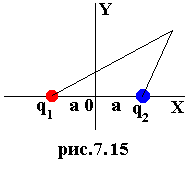
В качестве примера применения принципа суперпозиции рассмотрим задачу о нахождении поверхности нулевого потенциала для двух точечных зарядов. Так как задача симметрична относительно оси, соединяющей заряды, то будем искать линию нулевого потенциала в любой плоскости, проходящей через эту ось. Тогда согласно (6.22) и рис.7.15
|
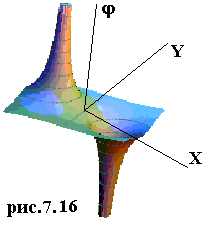
Данный потенциал как функция двух переменных для одинаковых по модулю разноименных зарядов показан на рис.7.16. |
 |
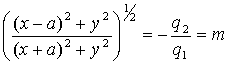 .
.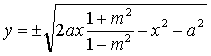 (7.30)
(7.30)С осью ОХ (y=0)эта кривая пересекается в точках
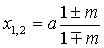 см. рис.7.17. Если теперь эту картину повернуть вокруг оси, соединяющей заряды, то получим поверхность нулевого потенциала. Попробуйте поискать эту же линию на рис.7.7. |
 |
12. Лапласиан скалярного поля.
В математической теории поля вводится следующее обозначение
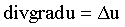 (7.32)
(7.32)где знак D является дифференциальным оператором второго порядка и называется оператором Лапласа.
По сути дела это его определение. Оператор не следует путать со знаком D- изменение. (Смешно, но значки абсолютно одинаковые).
13. Лапласиан в различных системах координат.
В декартовых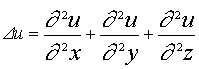
В цилиндрических
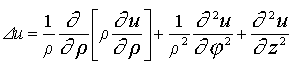
В сферических
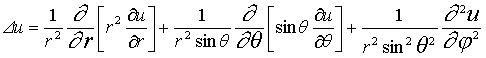
14. Уравнение Пуассона.
Легко получить, используя определение лапласиана, связь между напряженностью и потенциалом и теорему Гаусса, что
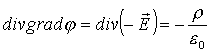
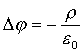 (7.37)
(7.37)Последнее равенство носит название уравнения Пуассона и связывает локальную характеристику поля – потенциал с его источниками, т.е. зарядами. Всюду, где нет зарядов, т.е. r=0, имеет место уравнение Лапласа
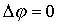
15. Пример на решение уравнения Пуассона.
Решим задачу о распределении потенциала внутри равномерно заряженного шара с помощью уравнения (7.37). Задача имеет сферическую симметрию, поэтому от оператора Лапласа остается только радиальный член.
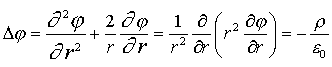
Дважды интегрируя, имеем
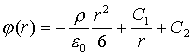 .
.Объемная плотность заряда очевидно равна
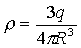
а постоянная С1=0, чтобы не было расходимости в центре шара. Тогда
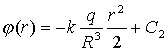 (7.41)
(7.41)Постоянную С2 мы пока находить не умеем, однако параболическая зависимость потенциала внутри шара получена верно (сравните с формулой 7.19 и рис.7.12).
16. Еще раз об операторах поля(математическое отступление).
Проведем некоторые математические обобщения.
Градиент — точки 1 и 2 замыкают кривую
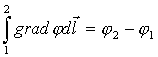
Ротор (формула Стокса) — кривая Lохватывает поверхностьS
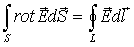
Дивергенция (формула Остроградского-Гаусса) — поверхность S охватывает объем V
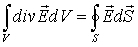
Физики очень любят краткие обозначения каких-либо сложных понятий. Поэтому они решили обозначать оператор
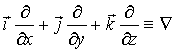 , (7.42)
, (7.42)где последний значок называется «набла-оператор» (оператор Гамильтона). Тогда
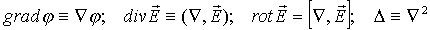 (7.43)
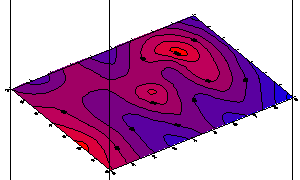
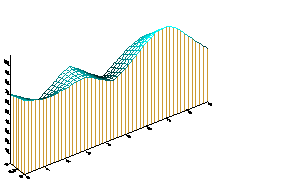
(7.43)17. Пример из географии(или о пользе межпредметных связей).

|
Приведем пример из географии. На нижнем рисунке показан оцифрованный фрагмент местности где-то вблизи Верхнедырюпинска. Хорошо видна горка, с которой так удобно обозревать окрестности (точка А), и впадина, по которой в дождливую погоду течет Дырюпкин ручей (линия BCD. По сути дела мы имеем функцию зависимости высоты от географических координат, т.е. функцию двух переменных h=h(x,y). Теперь подвигайте скроллингом. Вы увидите карту линий равной высоты, а еще выше векторное поле градиента. На четвертом рисунке показано сечение плоскостью EFGH. Правда, все это похоже на то, о чем мы говорили выше?! |
 |

|

|

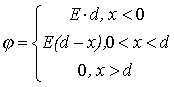 (7.14)
(7.14)